Реализация методических рекомендаций по обучению прикидке и оценке результатов вычислений в 5- 6 классах

На этом уроке после этапа актуализации знаний и объяснения решение задачи на нахождение процента от числа (задачи первого типа) учитель выписывает на доске так называемые «красивые проценты», нахождение которых наиболее простое и быстрое: 5%, 10%, 20%, 25%, 50%, 100%

Переводим проценты сначала в десятичную, а затем в обыкновенную дробь.

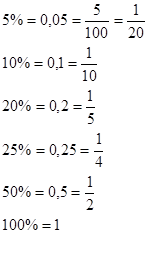
Учитель. Для того, чтобы найти 5,10,20,25,50 процентов, достаточно (судя по тем обыкновенным дробям, которые этим процентам соответствуют), число разделить на…

Ученик. 20, 10, 5, 4, 2 части

Далее при выполнении классной работы будем решать задачи первого типа (на нахождение процента от числа). Необходимо дать несколько задач, где встречаются «красивые проценты».

Задача.

Миша съел 75% всех конфет. Всего конфет было 56. Сколько конфет осталось?

Учитель, проходя по классу замечает того, кто уже начал решать задачу только что изученным «классическим» способом: число делим на сто, находим 1% и т.д. Ученик идет к доске и оформляет задачу.

Съел? шт. – 75%

Всего 56 шт. – 100%

Ост? шт. – ?%

Учитель. А можно ли эту же задачу решить проще?

Другой ученик. Да, узнаем, что осталось 100–75=25%, а 25% – это «красивый процент», поэтому число всех конфет достаточно поделить на 4.

Учитель. Иди к доске, посмотрим, кто решит задачу быстрее.

1 вариант

1) 56:100 = 0,56 – 1%

2)конфет осталось

2 вариант

1) 56:4=14 конфет осталось

Второй ученик справится быстрей.

Таким образом школьникам при помощи мини – соревнования наглядно показана быстрота, красота и удобство использования рационального способа решения задачи.

Вычислять быстро, подчас на ходу – это требование времени. Числа окружают нас повсюду, а выполнение арифметических действий над ними приводит к результату, на основании которого мы принимаем то или иное решение. Понятно, что без вычислений не обойтись как в повседневной жизни, так и во время учебы в школе.

В ходе анализа научно–методической литературы были выделены различные приемы быстрого счета, приведено разделение этих приемов на общие и специальные, а также рассмотрены приемы, описанные различными математиками (С.А. Рачинским, Я. Трахтенбергом).

Помимо приемов устного счета в дипломной работе выделены приемы прикидки и оценки результата вычислений. Нами были обозначены лишь те приемы, которые доступны для понимания и усвоения учащихся 5–6 классов, а также связаны с теоретическим содержанием курса математики 5-6 классов и соответствуют идее, которая прослеживается в учебнике Виленикина Н.Я и др., который был использован при составлении фрагментов уроков.

В 5–6 классе для учеников самым трудным является этап самоконтроля. Выполнение контрольной работы быстрее всех, даже не задумываясь о возможности ошибки, является психологической особенностью школьников этого возраста. А обучение прикидке и оценке результата вычислений помогает ученикам найти неточности, благодаря тому, что они учатся видеть заведомо неверный ответ.

Формируя каждый из компонентов, мы формируем вычислительную культуру ученика в целом.

Эффективное формирование вычислительной культуры учащихся зависит от правильного сочетания форм и методов обучения учащихся, в основе которого лежит и учет психологических особенностей.

На основе анализа существующих методов, форм и средств обучения для формирования вычислительной культуры школьников, а в частности формирования прикидки и оценки результата вычислений, был выделен в качестве основного эвристический метод, и в параграфе четвертом подробно описано сходство этого приема с приемами прикидки.

При осуществлении обучения учащихся в 5–6 классах в соответствии с темой дипломной работы используются общие и специальные приемы устного счета, приемы рассуждений, приемы угадывания при обучении прикидке и оценке результата вычислений, полезны также будут наглядность и соревновательность.

В дипломной работе представлены разработанные автором 7 фрагментов уроков. В каждом фрагменте указан этап применения того или иного приема, обычно он следует после актуализации знаний или этапа устного счета.

Было установлено, что задачи на прикидку и оценку результатов вычислений встречаются не только в рассмотренных в работе учебниках математики для 5–6 классов, но и, что является наиболее важным, в заданиях итоговой государственной аттестации и единого государственного экзамена. Были приведены примеры таких заданий и способы их решения. А также, неотъемлемой частью является то, что обучение прикидке и оценке результатов вычислений считается обязательным, в соответствии с государственным стандартом.

Другое о образовании:

Работа с коллективом родителей
Большие возможности предоставляет работа с коллективом родителей: широкая педагогическая информация, об мен опытом, создание в необходимых случаях общественного мнения, привлечение родителей к участию в жизни класса. Эта работа ведется в двух направлениях: повышение педагогической культуры родителе ...

Современная система образования США
Современная система образования США, сложившаяся под влиянием исторических, экономических и социальных факторов, характеризуется рядом особенностей, которые во многом отличают ее от западноевропейских стандартов. В США отсутствует единая государственная система образования, каждый штат вправе опред ...

Проблемы родителей, имеющих ребенка с ограниченными возможностями
Семья, как и человек, является основной ценностью государства. Снижение в силу тех или иных причин социальной ценности отдельных категорий семей, находящихся в жизненно трудной ситуации, ограничивает раскрытие потенциальных возможностей человека. В подобной ситуации возникает комплекс проблем, сред ...