Реализация методических рекомендаций по обучению прикидке и оценке результатов вычислений в 5- 6 классах
Пункт в)
Учитель. В этом пункте какие числа делим?
Ученик. Обыкновенные дроби.
Учитель. С чем сравниваем?
Ученик. С делимым.
Учитель. А мы с вами выяснили, что результат такого деления всегда больше или меньше делимого?
Ученик. Всегда больше! Поэтому ![]()
Пункт г)
Учитель. Какие числа делим?
Ученик. Смешанное число на правильную дробь.
Учитель. Такой случай аналогичен…
Ученик. Случаю деления натурального числа на правильную дробь, значит результат будет больше делимого, то есть больше, чем само смешанное число
![]()
Таким образом при дальнейшем решении задач ученикам будет легче заметить ошибку, так как они сумеют оценить правильность своего ответа, прикинув каким будет результат, зная что должно получатся в том или ином случае деления.
Фрагмент урока №6
Класс
: шестой
Тема
: «Свойства действий с рациональными числами»
Тип урока
: закрепление нового материала
Цель фрагмента
: формирования умения отыскания наиболее короткого и удобного пути вычисления, основываясь на свойствах рациональных чисел
Учебник
: Виленкин Н.Я и другие
На тему «Свойства действий с рациональными числами» отводится три часа. Этот второй урок по данной теме. На первом уроке были освещены основные свойства действий с рациональными числами и выполнены вводные упражнения на применение этих свойств. На втором уроке планируется выполнение тренировочных упражнений, некоторые из которых позволяют формировать вычислительную культуру рациональных вычислений, пользуясь уже известными свойствами.
После повторения свойств действий с рациональными числами и определения рационального числа вспоминаем, что эти свойств призваны прежде всего «упростить нам жизнь», делать наши вычисления на порядок проще. Но для этого нужно быть очень внимательным, и перед тем как приступать к вычислениям, посмотреть, а нельзя ли что-нибудь упростить.
Среди номеров, выбранных для классной работы, учитель предлагает выполнить номер 1206.
№1206. Выбрав удобный порядок вычислений, найдите значения выражений:
а)![]()
б)![]()
в) ![]()
Учитель. В каждом из пунктов встречаются вперемешку действия с десятичными, обыкновенными дробями и смешанными числами. Удобно ли нам будет выполнять действия «в лоб», последовательно складывать или вычитать, находя при этом общий знаменатель и т.п.?
Ученик. Нет! Применив распределительное свойство, можно поменять местами пары чисел таким образом, чтобы в одно скобке оказались десятичные дроби, а далее следовали обыкновенные дроби или смешанные числа с одинаковыми знаменателями (или наоборот).
Пункт а)
Это самый простой пример, школьники без затруднений находят пары «удобных чисел» и выполняют необходимые действия.
![]()
Пункт б)
В этом примере на первый взгляд только одна «удобная пара», но в процессе решения можно заметить появление еще одной.
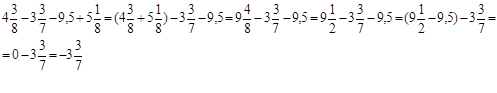
Пункт в)
Учитель. Как проще выполнять действия в этом примере?
Ученик. Все дроби со знаменателем 14 запишем сначала, а затем – все дроби со знаменателем 12.
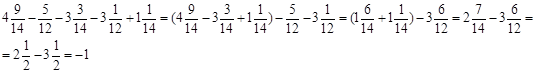
Таким образом на протяжении всей темы, ученики учатся максимально (насколько это возможно) упрощать сначала числовые, а затем буквенные выражения, что приводит к упрощению вычислений и меньшим затратам времени и сил.
Фрагмент урока №7
Класс
: пятый
Тема урока
: «Проценты»
Тип урока:
комбинированный урок
Цели урока
: наглядно, используя соревновательный момент, показать более короткий способ нахождения «красивого процента» от числа
Учебник:
Виленкин Н.Я и другие
Всего на данную тему отводится 5–6 часов. Это второй урок по теме: «Проценты».
На первом уроке было введено понятие процента и представление его в виде десятичной дроби и, наоборот, представление дроби в виде процента, находили 1% от числа и число по его одному проценту.
Другое о образовании:
Методы и приемы эстетического воспитания школьников на уроках искусства
В основе методики эстетического воспитания лежит совместная деятельность педагога и ученика по развитию у него творческих способностей к восприятию художественных ценностей, к продуктивной деятельности, осознанного отношения к социальной, природной, предметной среде. Успех этой работы во многом опр ...
Организация уроков литературного чтения по
развитию нравственных качеств у младших школьников
Процесс нравственного воспитания есть общественное осуществление педагогически целенаправленной деятельности по организации нравственной подготовки подрастающих поколений, результатом которой является усвоение растущим человеком социального морального опыта и формирование нравственных качеств его л ...
Японские вузы
Поскольку будущее ученика по окончании средней школы зависит от оценки его способностей при поступлении в престижную школу второй ступени и университет, большинство учащихся всех классов несколько вечеров в неделю посещают специальные подготовительные учебные заведения «дзюку». Считается, что будущ ...

