Сравнительный анализ методик

Как движется лодка относительно этих двух систем?

Наблюдатель на плоту, двигаясь вместе со «своей» системой координат по течению, видит, что лодка удаляется от него к противоположному берегу все время перпендикулярно течению. Он видит это и в точке А, и в точке В, и в любой другой точке. А когда через некоторое время плот окажется в точке С, лодка достигнет противоположного берега в точке С’. Относительно подвижной системы координат (плота) лодка совершила перемещение . Разделив его на , подвижный наблюдатель получит скорость лодки относительно плота:

.

Совсем другим представится движение лодки неподвижному наблюдателю на берегу. Относительно «его» системы координат лодка за то же время совершила перемещение . За это же время подвижная система отсчета вместе с плотом совершила перемещение (лодку, как говорят, «отнесло» вниз по течению). Схематически перемещения лодки показаны на рисунке. [3]

Далее в этом параграфе вводятся формула сложения перемещений

и формула сложения скоростей

,

а так же, чему равна скорость тела относительно неподвижной системы координат.

Мы видим, что и перемещение и скорость тела относительно разных систем отсчета различны. Различны и траектория движения ( – относительно подвижной системы и – относительно неподвижной). В этом и состоит относительность движения.

Далее мы переходим к рассмотрению преобразований Галилея в курсе общей физики.

С объяснения этого понятия начинается изучение принципа относительности Галилея. Сопоставляются описания движения частицы в инерциальных системах отсчета и, движущихся друг относительно друга со скоростью (рис. 6).

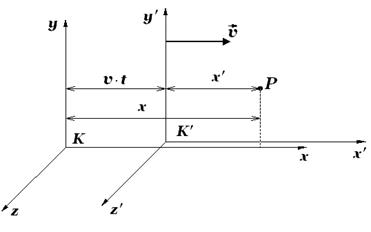
Рис. 6

Для простоты выбираются оси координат так, как показано на рисунке. Отсчет времени начинается с того момента, когда начала координат и совпадали. Тогда координаты и произвольно выбранной точки будут связаны соотношением . При сделанном выборе осей и . В ньютоновской механике предполагается, что время во всех системах отсчета течет одинаково; поэтому . Таким образом, получается совокупность четырех уравнений:

, , , ,

называемых преобразованиями Галилея. Эти уравнения позволяют перейти от координат и времени одной инерциальной системы отсчета к координатам и времени другой инерциальной системы.

Следуя по программе, далее рассматриваются инерциальные системы отсчета и первый закон Ньютона.

Законы механики одинаково выглядят во всех инерциальных системах отсчета.

Затем необходимо познакомиться с классическим законом сложения скоростей. Мы знаем, что компоненты скорости частицы в системе определяются выражениями

Другое о образовании:

Развитие личности и положительных качеств ребенка дошкольного возраста
Проблема развития личности ребенка дошкольного возраста раскрыта в психолого-педагогических исследованиях Л.И. Божович, Л.С. Выготского, В.В. Давыдова, А.В. Запорожца, Я.Л. Коломинского, Т.С. Комаровой, А.Н. Леонтьева, В.И. Логиновой, Д.Б. Эльконина. Ученые утверждают, что в дошкольном возрасте про ...

Речевые ошибки и причины их возникновения
В устной и письменной речи младших школьников встречается много ошибок, которые в методике обучения русскому языку называют речевыми. К определению «речевая ошибка» ученые подходят по-разному. В работах М. Р. Львова под речевой ошибкой понимается «неудачно выбранное слово, неправильно построенное п ...

Критерии и характеристики сформированности готовности к профессиональному самоопределению
Говоря о профессиональном самоопределении и выборе профессии учеников 8 – 11 классов, следует отметить существование определенных критериев и их характеристик сформированности у старшеклассников готовности к профессиональному самоопределению. Проявлениями критериев сформированности готовности к про ...