Идея относительности в кинематике

Записывают уравнение движения для второго тела:

; ;

; ; ; .

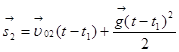Уравнение координаты для второго тела:

,

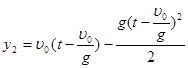где – координата второго тела в любой, произвольный момент времени, – время движения первого тела до момента бросания второго тела.

В момент встречи тел в полете их координаты равны, т. е. (условие встречи).

Приравняв координаты и решив полученное уравнение относительно , получают: – время, прошедшее от момента бросания первого тела до встречи его со вторым.

Так как от момента бросания первого тела до момента бросания второго тела прошло время , то ответ на вопрос задачи такой: , т. е. время, прошедшее до момента встречи тел от момента бросания второго тела равно .

Решение 2. За начало отсчета времени выбирают момент бросания второго тела (рис. 2), остальные условия те же, что и в первом решении.

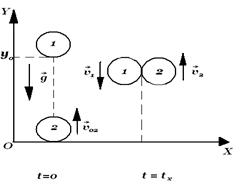
Рис. 2

Записывают уравнение движения для первого тела:

; ; ; ; ; .

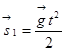Уравнение координаты для первого тела:

,

где – координата первого тела в любой, произвольный момент времени.

Записывают уравнение движения для второго тела:

; ; ; ; .

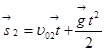Уравнение координаты для второго тела:

,

где – координата в любой, произвольный момент времени.

Решают систему уравнений при условии, что (условие встречи) и в данном решении по сравнению с первым сразу получают ответ на вопрос задачи: .

Решение 3. Выбирают систему отсчета так, чтобы телом отсчета было второе тело, которое еще находится на Земле. Совместим начало отсчета координаты со вторым телом, ось направим вверх. За начало отсчета времени принимают момент бросания второго тела. Первое тело движется относительно второго тела в этой системе отсчета равномерно и прямолинейно. Первоначальное расстояние первого тела от начала координат . Двигаясь равномерно и прямолинейно в этой системе отсчета со скоростью , первое тело пройдет это расстояние за время

Другое о образовании:

Методическая разработка занятия по иностранному языку
Многогранная деятельность учителя предполагает составление им сценария урока, опору его деятельности или рабочий план урока, который будет носить субъективный характер. В плане учитель прогнозирует свою деятельность в единстве с деятельностью учащихся, регулируя ее. При этом он творчески подходит к ...

Условия повышения эффективности системы работы с одаренными студентами
Наличие магистратуры как средства отбора талантливых студентов, как образовательной ступени, позволяющей вести обучение на высоком уровне трудности, совмещать разнообразные формы организации учебного процесса и научной деятельности: научные семинары, студенческие исследовательские лаборатории, защи ...

Методика использования контрольно-аттестационного комплекта на занятиях по другим дисциплинам экономического направления
Цель контрольного процесса на занятиях экономического направления: убедиться, что приобретенные знания и умения по определенным дисциплинам соответствуют предъявляемым требованиям. Место, в которое целесообразно поместить проверку в процессе обучения, определяется ее целями. Как было установлено, о ...