Идея относительности в кинематике

Покажем, как были получены эти результаты, проведя решение задачи.

Решение. Для решения задачи используем классический закон преобразования (сложения) скоростей: скорость тела в неподвижной системе отсчета равна сумме скорости тела в подвижной системе отсчета и скорости самой подвижной системы отсчета: . Движение происходит вдоль оси ОХ и соответственно закон преобразования (сложения) скоростей записывается через проекции скоростей на ось ОХ: .

1. В системе отсчета, связанной с Землей, скорости заданы в условии задачи и их проекции на ось ОХ соответственно равны: ; м/с; м/с.

2. В системе отсчета, связанной с мотоциклистом:

; м/с = – 20 м/с;

; м/с – 20 м/с = – 15 м/с;

; м/с – 20 м/с = 0.

3. В системе отсчета, связанной с велосипедистом:

; - 5 м/с = – 5 м/с;

; м/с – 5 м/с = 15 м/с.

Сведения в таблицу полученных результатов дает наглядное представление об относительности скорости, о роли системы отсчета в определении последней.

Целесообразно показать, что все системы отсчета в кинематике равноправны, но следует выбирать такую систему отсчета, которая приводит к рациональному решению задачи. Для этого целесообразно решить одну и ту же задачу в разных системах отсчета.

Задача.

Тело брошено вертикально вверх со скоростью . Когда тело достигает верхней точки траектории, из того же места и с той же скоростью вертикально вверх брошено второе тело. Через сколько времени от момента бросания второго тела произойдет встреча этих тел?

Задачу решают в системе отсчета, связанной с Землей, и в системе отсчета, связанной с одним из тел.

Решение 1. За начало отсчета координаты принимают место бросания тел на Земле. Ось OY направляют вертикально вверх. За начало отсчета времени принимают момент бросания первого тела (рис. 1).

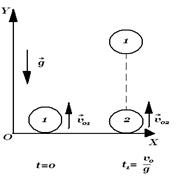
Рис. 1

Записывают уравнение движения для первого тела:

; ; ; ; .

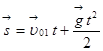Уравнение координаты для первого тела:

,

где – координата первого тела в любой, произвольный момент времени.

Другое о образовании:

Методические разработки по теме: "Аммиак. Соли аммония"
Урок разработан в форме исследования с целью получения новых знаний с использованием проблемного и дифференцированного подхода. Форма урока выбрана не случайно. Проблема использования аммиака и солей аммония, их свойств достаточно сложна, но посильна для девятиклассников. Учитель направляет с помощ ...

Особенности двигательного развития детей
Движение для ребенка – это универсальное проявление жизнедеятельности, на различные раздражения он реагирует прежде всего движением (например, отдергивание руки при ожоге пальца, сосательные движения младенцев при раздражении губ и щек и т.д.). Вместе с тем от рецепторов мышц, сухожилий, суставов, ...

Наблюдение как метод формирования эстетических чувств старших дошкольников
В период дошкольного детства ребенок открывает мир природы. Поддерживая естественный интерес дошкольников ко всему живому, педагог ведет детей от знакомства с природой к ее пониманию, вызывает желание заботиться о растениях и животных, воспитывает основы экологической культуры, любознательность, сп ...