Преобразования Галилея

Преобразования Галилея –

это уравнения, связывающие координаты и время некоторого события в двух инерциальных системах отсчета. Событие определяется местом, где оно произошло (координаты ), и моментом времени , когда произошло событие. Событие полностью определено, если заданы четыре числа: – координаты события.

Пусть материальная точка в системе отсчета в момент времени имела координаты , т. е. в системе заданы координаты события – .

Найдем координаты этого события в системе , которая движется относительно системы равномерно и прямолинейно вдоль оси со скоростью.

Выберем начало отсчета времени так, чтобы в момент времени начала координат совпадали. Оси и направлены вдоль одной прямой, а оси и , и – параллельны.

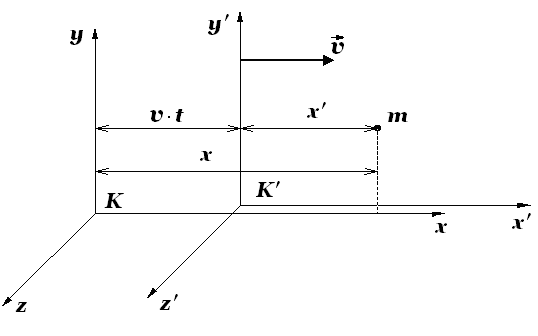
Рис. 3

Тогда из рисунка очевидно:

.

Кроме того, ясно, что для наших систем координат

,

.

В механике Ньютона предполагается, что

,

т. е. время течет одинаково во всех системах отсчета.

Полученные четыре формулы и есть преобразования Галилея:

,

,

,

.

3. Программы

Курс общей физики

1.

Физические преобразования координат.

2.

Инерциальные системы отсчета, первый закон Ньютона.

3.

Классический закон сложения скоростей.

4.

Инвариантность длины, интервала времени, ускорения.

5.

Абсолютный характер понятия одновременности.

Курс школьной физики

1.

Относительность механического движения.

2.

Относительная, абсолютная, переносная скорости.

Другое о образовании:

Методы работы с аутентичными текстами
Аутентичные тексты, используемые в учебном процессе, призваны акцентировать внимание учеников на типичных сторонах действительности страны изучаемого языка с целью знакомства с бытовыми и культурными реалиями жизни и особенностями речевого поведения носителей изучаемого языка. Последовательность ра ...

Так что мы можем подразумевать под понятием “нетрадиционная форма урока”? О.В.Трофимова дает следующее определение: “НФУ – это интерактивные формы урока, характеризующиеся субъект – субъектной позиц
Техническое творчество является непосредственным трудом по материализации в своеобразной форме законов и свойств природных явлений. Будут специфической формой мыслительной деятельности, оно способствует развитию знаний человека об объективном мире. Техническое творчество позволяет не только отражат ...

Педагогическая организация восприятия искусства школьниками
Взаимодействие ребенка и любого вида искусства прежде всего начинается с восприятия. Произведение искусства достигает своей воспитательной, образовательной цели, когда оно непосредственно воспринято школьником, когда освоена его идейно-художественная сущность. Очень важно уделять особое внимание им ...